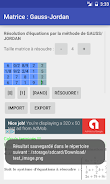
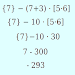L'APP Gauss-Jordan est un outil puissant pour résoudre des équations à "n" inconnues à l'aide de la méthode Gauss-Jordan, également connue sous le nom de "pivot gaussien". Il gère différents formats de nombres, notamment les décimaux, les entiers et les fractions, fournissant des résultats sous forme fractionnaire et décimale.
L'application va au-delà des solutions simples en proposant des explications étape par étape du processus de résolution, permettant aux utilisateurs de comprendre la logique derrière les résultats. Pour plus de commodité, les utilisateurs peuvent enregistrer les résultats sous forme d'images pour une référence ou un partage facile.
Au-delà de la résolution d'équations, l'application Gauss-Jordan peut également calculer des équations polynomiales basées sur des points donnés, fournissant ainsi un graphique correspondant pour la représentation visuelle. Il améliore encore sa fonctionnalité en simplifiant les fractions et en décomposant les entiers.
Caractéristiques principales :
- Résout les équations avec "n" inconnues à l'aide de la méthode Gauss-Jordan.
- Gère les nombres décimaux, entiers et fractionnaires.
- Fournit les résultats aux formats fraction et décimal.
- Propose des explications étape par étape de la solution processus.
- Permet aux utilisateurs d'enregistrer les résultats sous forme d'images.
- Calcule des équations polynomiales en fonction de points donnés et les affiche avec un graphique correspondant.
- Simplifie les fractions et décompose les entiers.
Avantages :
L'application Gauss-Jordan fournit une interface conviviale et un ensemble complet de fonctionnalités pour résoudre des équations, travailler avec des fractions, des décimales et des nombres entiers. Sa capacité à fournir des explications étape par étape et des représentations visuelles en fait un outil idéal tant pour l'apprentissage que pour les applications pratiques.