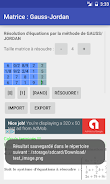
Ứng dụng Gauss-Jordan là một công cụ mạnh mẽ để giải các phương trình có ẩn số "n" bằng phương pháp Gauss-Jordan, còn được gọi là "trục Gaussian". Nó xử lý các định dạng số khác nhau, bao gồm số thập phân, số nguyên và phân số, cung cấp kết quả ở cả dạng phân số và dạng thập phân.
Ứng dụng còn vượt xa các giải pháp đơn giản bằng cách đưa ra các giải thích từng bước về quy trình giải pháp, cho phép người dùng hiểu logic đằng sau kết quả. Để thuận tiện hơn, người dùng có thể lưu kết quả dưới dạng hình ảnh để dễ tham khảo hoặc chia sẻ.
Ngoài việc giải phương trình, APP Gauss-Jordan còn có thể tính toán các phương trình đa thức dựa trên các điểm đã cho, cung cấp biểu đồ tương ứng để thể hiện trực quan. Nó nâng cao hơn nữa chức năng của mình bằng cách đơn giản hóa phân số và phân tách số nguyên.
Các tính năng chính:
- Giải phương trình với ẩn số "n" bằng phương pháp Gauss-Jordan.
- Xử lý các số thập phân, số nguyên và phân số.
- Cung cấp kết quả ở cả định dạng phân số và thập phân.
- Cung cấp giải thích từng bước về quy trình giải pháp.
- Cho phép người dùng để lưu kết quả dưới dạng hình ảnh.
- Tính phương trình đa thức dựa trên các điểm đã cho và hiển thị chúng dưới dạng biểu đồ tương ứng.
- Đơn giản hóa phân số và phân tích số nguyên.
Lợi ích:
Ứng dụng Gauss-Jordan cung cấp giao diện thân thiện với người dùng và bộ tính năng toàn diện để giải phương trình, làm việc với phân số, số thập phân và số nguyên. Khả năng cung cấp các giải thích từng bước và trình bày trực quan khiến nó trở thành một công cụ lý tưởng cho cả ứng dụng học tập và thực tế.