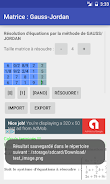
The Gauss-Jordan APP is a powerful tool for solving equations with "n" unknowns using the Gauss-Jordan method, also known as "Gaussian pivot". It handles various number formats, including decimals, integers, and fractions, providing results in both fractional and decimal forms.
The app goes beyond simple solutions by offering step-by-step explanations of the solution process, allowing users to understand the logic behind the results. For added convenience, users can save the results as images for easy reference or sharing.
Beyond equation solving, the Gauss-Jordan APP can also calculate polynomial equations based on given points, providing a corresponding graph for visual representation. It further enhances its functionality by simplifying fractions and decomposing integers.
Key Features:
- Solves equations with "n" unknowns using the Gauss-Jordan method.
- Handles decimal, integer, and fractional numbers.
- Provides results in both fraction and decimal formats.
- Offers step-by-step explanations of the solution process.
- Allows users to save results as images.
- Calculates polynomial equations based on given points and displays them with a corresponding graph.
- Simplifies fractions and decomposes integers.
Benefits:
The Gauss-Jordan APP provides a user-friendly interface and a comprehensive set of features for solving equations, working with fractions, decimals, and integers. Its ability to provide step-by-step explanations and visual representations makes it an ideal tool for both learning and practical applications.